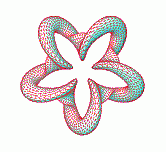Torsion is a difficult property to observe directly. It has a sign, which distinguishes rolling to the left from rolling to the right. We only visualize the unsigned quantity, which we transform using f(x)=1+R*|x|. The cross-section is an area preserving ellipse with aspect ratio equal to f of the torsion at that point of the curve. The ellipse does not rotate within its frame and the major axis is aligned with the normal vector, N (s).

Note that if the number of times the curve winds around the meridian is small but not too small, the torsion gets rather large when the curve passes the narrow neck of the torus. This is reflected by a skinny ellipse generating a pronounced ridge on the tube. We chose to use two numbers to name each object, encoding the number of times the curve winds around the length and around the meridian of the torus.

(2, 1/2)

.stl file

(1, 1)

.stl file

(1, 2)

.stl file

(1, 3)

.stl file

(1, 6)

.stl file

(1, 7)

.stl file

(1, 8)

.stl file

(2, 8/2)

.stl file

(2, 9/2)

.stl file

(2, 10/2)

.stl file