Complexity aspects of dynamical processes
We already worked on one process. You can read the paper here.
Motivation
Imagine that you want to start a viral campaign. People will transmit the information themselves, and you know how they are excited about your product. The only thing you need to do is get the first few customers yourself. But whom should you convince?
In the previous post, I explained the spread of cooperation. So far, everyone uses simulation to get some results. Is there another way?
Generally, complexity results tell us what is possible and where to use crude simulation.
Complexity classes
To determine the complexity, you need to show the upper and lower bound. One is usually trivial. The other is harder. A complicated part is also determining which is the easy half.
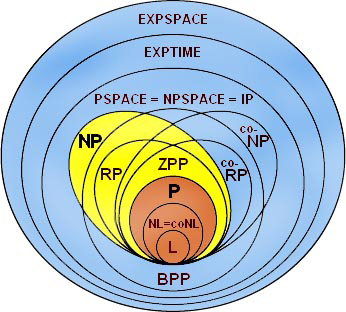
There are plenty of classes where we can put our problem (you can see it in the picture). We use the three most basic: fast, complex, and impossible (if you know about complexity these are P, NP, and PSPACE).
Fast (P)
Fast class (P) corresponds to problems solvable on modern computers. To prove that a problem is in P, we provide an algorithm. It is usually the hard part. For instance, for stochastic games we expect them to be fast but we don't know the algorithm.
For P, we usually don't prove lower bound. We try to make the algorithm as efficient as possible. Only after the problem was examined so well that a new algorithm does not decrease the running time (the solvers, even if they are not the most efficient, they are heavily optimized in practice), then we might think about the lower bound.
Complex (NP)
Complex class (NP) cannot be solved fast. (There might be cases where it's possible, but this is a realm of parameterized complexity). The lower bound here is usually tricky. We need to imagine a problem about which we know is hard. Then we will change it bit by bit, and then it needs to result in our problem.
A concrete example of this is saying: Going from Vienna to IST (known hard problem) is at least as hard as going to Vienna from Klosterneuburg (a problem in question). The solution is:
- Show that going from Vienna to IST goes through Klosterneuburg.
- Show that you can reverse the path (going from A to B is the same as going from B to A).
An algorithm for solving problems from NP is usually not complicated to find. NP class uses nondeterminism, which means we can guess the solution and then verify the solution works. Unfortunately, we cannot guess a solution for every problem.
Impossible (PSPACE)
If we prove the problem is in PSPACE, we have no hope for a good algorithm. The only thing to do if we want to know what is the result, we need to simulate it and hope that the simulation ends quickly.
The upper bound is easy to prove. PSPACE means that we have a computer that has a large (but not infinite) memory, and it can run for a very long time. So the algorithm usually simulates everything or tries all possibilities.
The lower bound is trickier. We can use the same trick as in the proving NP, have a problem, and then change it. Another approach is to create a computer with a process that can compute by itself.
In the paper about the game of life, we create such a computer using nodes that change their state by a simple rule.
The complexity of spatial games
We created a construction for the prisoner's dilemma that shows the complexity. Everything is almost done, and we will publish it shortly.
I think that finishing the paper would mean abandoning the topic. It's more interesting to work on something positive than negative. I also don't know about a good question that might be interesting to a wide audience.
What I'm proud about are our videos. You will be able to see parts of our construction.
Signed graphs
Definition
We have a graph: Every two vertices are connected by an edge with a sign, either + or - (friendship or enmity). We say that three vertices (triangle) are unbalanced if it contains one or three negative signs.
We run the following process: We select an unbalanced triangle and flip (change sign) of one edge selected by some algorithm. It makes the triangle balanced (but can break some other triangles). We continue until there are no unbalanced triangles.
Motivation
If your two friends start arguing, what can you do? You can either try to make them friends again or side with one and forget about the other. It corresponds to the dynamic.
Signed graphs describe this situation. In a graph, every two vertices (people) are either friends or enemies. Then the vertices (people) are trying to solve their problem locally.
Moreover, signed graphs have physical motivation. It describes how the system goes to the position with the lowest energy, and it should correspond to something real, but I don't know what exactly. (It's somewhat hard to find the motivation.)
The problem is interesting, but we also do it because it is synchronous with other problems, mainly about spreading in the network. Signed graph dynamics tells us how to change the underlying graph, where some different processes might be happening.
Question
We want to design an algorithm that selects an unbalanced triangle and possibly looks at other edges in the graph, and based on that, it flips one edge. The algorithm aims to quickly get to a position without unbalanced triangles.
The algorithm should not look at too many other edges. People also do not consider every friend of a potential friend to decide if they like him or not. That is the biggest constraint.
What is known
Positions that do not contain any unbalanced triangle have two types. Either everyone is a friend with everyone else (utopia), or people are split into two groups that do not like each other.
We can get to the utopia easily: every time we select an unbalanced triangle, we flip the enmity edge. It is boring.
If we look only at the unbalanced triangle and no other edges, we cannot do anything smarter than flip a random edge. Then we need almost infinite time to balance the graph (exponential in the number of vertices).
If we take an unbalanced triangle and look at all friendships of its participants, we can do better. Here, they described one such algorithm that is supposedly fast.
We noticed that the algorithm might get stuck. The authors don't mention that in the paper. So we researched the idea and proved few things about it.
Unfortunately, when we were writing our paper, we found that it is already known, and the authors do not speak about it (even though they know about it).
What we found
We created a better algorithm that looks at the same number of edges as the previous algorithm that can get stuck. Ours cannot get stuck and is faster. We also quantified how bad are other algorithms.